在设计和调整线性运动系统时,第一个步骤是确定什么类型移动剖面的应用程序需要,因为这决定了如何计算速度和加速度,并对它们的平均值和最大值有重要影响。
速度和加速度是任何线性运动应用的两个基本方面。它们影响导向系统上的力,驱动组件所需的扭矩,在某些情况下,它们立即缩小了可以考虑的导轨和驱动器的选择范围。举个例子:如果您的应用程序要求5米/秒的最大速度,滚珠或丝杠可能是不可能的,您需要考虑皮带、齿条和齿轮或直线电机驱动。
即使是最复杂的过程也是基于这两种基本的运动轨迹,它们是三角形和梯形,因其速度-时间图的形状而得名。
三角形移动剖面
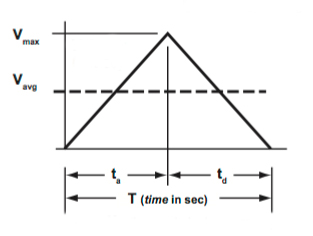
三角形运动剖面的基本前提是加速到最大速度,然后立即减速,加速度和减速在时间和距离上都相等。换句话说,如果你想在最快的时间内从这里移动到那里,你会使用三角形移动剖面。决定任何移动变量——时间、速度、加速度或距离——都是基于三角形的几何形状。下面是三角形运动剖面的一些常见方程。
如何计算平均速度
由于加减速时间是相等的,并且不存在匀速时间,平均速度就是总距离除以总时间:
![]()
如何计算最大速度
最大速度是三角形的高度或峰值,是平均速度的两倍:
![]()
如何计算加速度
加速度是三角形一侧的斜率(“上升比移动”)。这是最大速度除以加速度时间,加速度时间是总移动时间的一半:
![]()
其中t一个=½tt
如何计算总距离
行进的距离等于曲线下的面积。由于曲线是三角形,所以距离等于三角形的面积,即1 / 2 *底*高。因此,行进的总距离等于½*总时间(基数)*最大速度(高度),即:
![]()
如何计算加速度距离
同样地,在加速(或减速,因为它们相等)期间行进的距离,三角形左(或右)半部分的面积为½*加速时间(基数)*最大速度(高度),或:
![]()
三角形移动轮廓除了是从一个点到另一个点的整体最快选择外,还需要比梯形轮廓更低的加速度,这意味着驱动单元上的推力更小。
梯形移动剖面
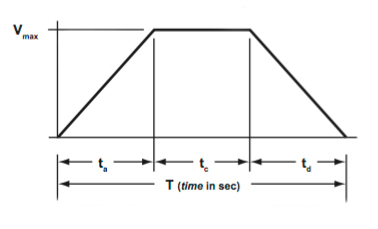
当应用程序需要加速到最大速度,然后在指定的时间或距离内以该速度移动时,使用梯形移动剖面。使用梯形移动轮廓的一些常见工艺有机械加工、点胶和喷漆。
梯形移动剖面的最简单形式,也就是下面例子中使用的,是1/ 3,1 / 3,1 /3剖面。在这种情况下,1/3的时间用于加速,1/3的时间用于匀速,1/3的时间用于减速。但是,如果您了解移动剖面的几何结构(本质上是两个三角形和一个矩形),那么无论时间段是否相等,您都可以计算必要的参数。
如何计算总距离
回想一下三角形移动剖面的讨论,行进的距离等于曲线下的面积。梯形运动剖面可以被视为三条曲线或段:加速度(三角形)、匀速(矩形)和减速(三角形)。因此,总行进距离为三条曲线的面积之和:
![]()
现在,插入三角形、矩形和另一个三角形的面积公式:
![]()
在每一段中,时间表示底,最大速度表示高度,则有:
![]()
重新排列给我们:
![]()
对于1/3,1/3,1/3剖面t一个= tc= td,每一段等于总时间t的1/3t.因此,方程为:
![]()
化简后,我们得到:
![]()
如何计算最大速度
如果需要确定最大速度,则可以将此公式重新排列为:
![]()
也可以表示为:
![]()
如何计算平均速度
与三角形移动剖面一样,梯形移动剖面的平均速度简单地是总距离除以总时间:
![]()
如何计算加速度
因为中间部分(矩形)只适用于恒定速度(零加速度),加速度的确定方法与三角形移动剖面大致相同。在这种情况下,使用左边三角形(表示加速)或右边三角形(表示减速):
![]()
如果我们把v代入,就可以得到一个基于距离和时间的方程马克斯根据上面的公式,插入1/3tt对于t一个:

简化后,加速度可表示为:

对于受益开云体育store于恒定速度周期的应用,梯形移动剖面提供了具有比三角形剖面更低的最大速度的优势。
虽然三角形和梯形的移动轮廓有很多变化,但了解它们的几何形状和方程将帮助你解决你可能遇到的任何版本。
s曲线移动剖面:在实际应用中,真正的梯形移动开云体育store轮廓很少使用,因为一种现象被称为混蛋.正如加速度是速度的变化率,加速度是加速度的变化率。因此,在梯形运动剖面中,当加速度开始或结束时,加速度是无穷大的。这导致了振荡,增加了沉降时间,降低了定位精度。减少颠簸的方法是平滑加速开始或结束的过渡,使梯形轮廓的尖角更像“s”。

如果你还没有计算完,看看我们的列表工程计算器.




这是关于如何计算伺服轴的预期运动轮廓的一些伟大的基本信息!